使用Gamry EIS300电化学阻抗谱软件进行等效电路模拟

引言

电化学阻抗谱（EIS）是分析复杂电化学系统的强有力工具。您可以浏览技术报告Basics of EIS，里面有对EIS的全面介绍。而那则技术报告中提及的大多数内容，本文将不再赘述。

本技术报告实际讨论了EIS数据分析常见的方法，给大家甚至是初学者提供从EIS阻抗谱理解电解池中物理过程的基本方法。本文特意回避了与EIS数据分析相关的复杂数学计算。

EIS基础知识

使用EIS时，您在一个广泛的交流频率范围内测试电解池的复阻抗。通常，系统的EIS阻抗谱由几个电解池元件和电解池特征促成。一部分可能的元件包括：

• 电极双电层电容

• 电极动力学

• 扩散层

• 溶液电阻

很遗憾，系统在任意给定频率的阻抗通常依赖于多个电解池元件，这大大地增加了EIS阻抗谱的分析难度。

分析EIS阻抗谱常用的方法是等效电路模拟，也就是将上述所提元件合并后对电解池进行建模。每个元件的行为用“经典”电学元件（电阻，电容，电感）和一些专门的电化学元件（例如Warbug扩散元件）来描述。

过程的第一步是凭知识或经验的猜测。您先预测觉得在电解池阻抗中起作用的系统元件。然后将这些元件建成一个等效电路模型。其中，将元件排列成逻辑的串并联组合是拟合研究成功的关键。

在模型中的每一个元件都有一个已知的阻抗行为。元件的阻抗依赖于元件的类型和表征该元件的参数值。举个例子，一个在频率f被正弦波激发的电容器的阻抗可由下式表示：

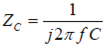(1)

Zc是复阻抗，j是√-1，f是频率（单位为赫兹），C是电容值（单位为法拉）。当用公式表示一个系统模型时，通常不知道系统中元件的参数值。举个例子，知道涂漆金属有一个涂层电容但并不知道这个电容的数值。

图形模型编辑器

包含在Gamry公司EIS300 电化学阻抗软件中的Echem Analyst Software软件有一个图形模型编辑器。您可以使用模型编辑器来形象化地建立一个等效电路模型。图1显示的是模型编辑器编辑的涂料模型，由EIS300提供。这个模型代表了金属表面失效的漆膜的物理现象的一种可能的电路元件。关于该模型的具体表述，请浏览前面提及的EIS的初级报告。

您可以使用图形模型编辑器来编辑相当复杂的电路。该方法的一个优点是您没有必要像使用一些老旧的拟合程序似的去处理令人困惑的电路编码。

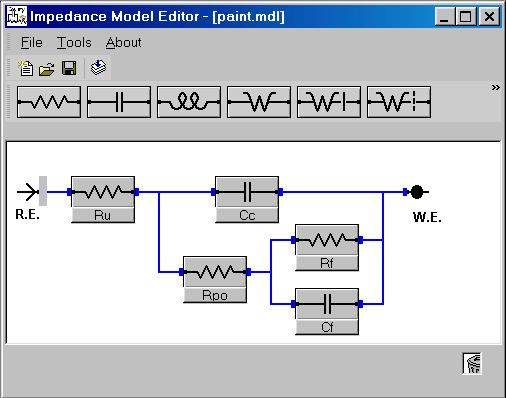
图1 模型编辑器

该技术报告中的第二个例子涉及的是当模型预先无法知晓时，EIS拟合成模型的问题。在这之前，我们将先讨论较简单的已知模型的数据拟合案例。

用模型拟合您的数据

一旦您觉得有一个模型代表了您的电化学系统，您使用非线性小二乘拟合程序去拟合实验数据。这个程序尝试将模型的阻抗谱和实验数据阻抗谱间的误差小化。

Echem Analyst里有两种拟合算法—Levenberg-Marquardt算法和Simplex算法。两种算法都会自动调整模型中元件的参数值以找到合适拟合值。拟合过程的数学细节不在该技术报告的讨论范围内。

等效电路拟合中一个比较困难的任务是确定模型参数的初始值。对于所有参数，两种算法都需要从初始值（常被称为种子值）开始。如果初始值与合适值相去甚远，优化程序可能无法获得合适拟合值。该技术报告的第一个例子论证了这一问题。

例1：与涂层金属相匹配的仿真数据

这个例子讨论了当模型已知的的数据拟合。为了保证一个良好的拟合结果，数据用一个由电学元件组成的仿真电解池来记录。各元件被分布在涂层模型中，如图1所示。

图2显示的是Bode形式的原始EIS阻抗谱。因为Nyquist曲线中缺乏频率信息比较难估算电容值，Gamry建议您用Bode曲线做拟合参数的初始估算。

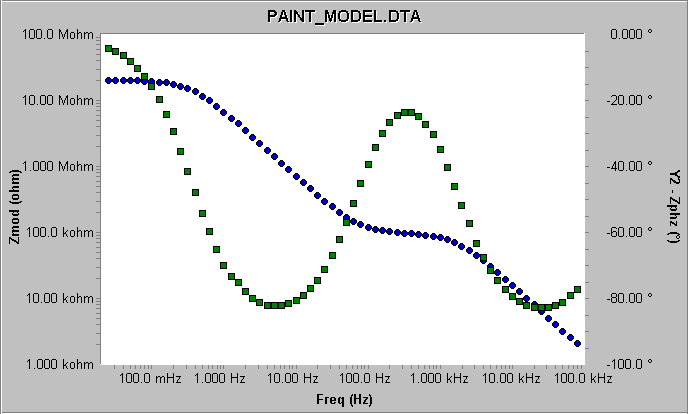
图2 涂层模型仿真电解池的原始阻抗谱

如果您用该涂层模型拟合数据时，没有调节参数的“初始值”（或按了Reset恢复到默认值），您可能会得到一个匹配错误的信息或者一个较差的拟合结果（图3）。拟合结果的数值大小（蓝色）和相位（绿色）都无法与数据较好地吻合。

这个错误是由不好的模型参数初始值造成的。Echem Analyst EIS分析中的拟合算法需要初始值在终值的一到两个数量级范围内才能正确地进行拟合。当初始值与合适值相去甚远时导致的拟合不稳定不是EIS300*的现象。其他EIS模型拟合程序同样需要初始值具有这样的精确度。

所以，如何估算初始值呢？这需要一个计算器，还需要您对电路中元件的表现有一定的了解。基本上，我们会尝试找到EIS曲线中模型阻抗由一种元件所控制的区域，然后计算在该频率处元件的近似值。

测试图1中的模型。请记住电容的阻抗在高频时接近于0，在低频时接近于无限大。低频时，模型中电容的阻抗非常得高。Cc和Cf都与电阻并联。当电容阻抗较高时，电阻阻抗是决定因素。在图1中的低频，阻抗大约是10⁷欧姆，相位角接近于0º（表现为电阻）。这是Rμ，Rp和Rf的总和。假设Rf>Rp>Rμ，您可以估算Rf是10⁷欧姆。至此，您就拥有了您的第一个初始值！

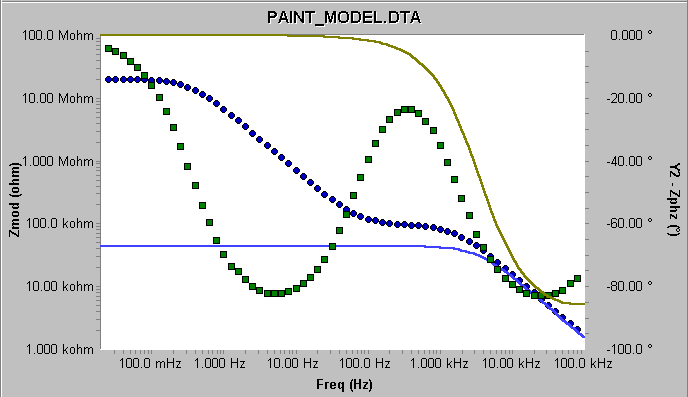
图3 将所有初始值重置成默认值的拟合

1Hz以上的阻抗降起因于Cf。10Hz处，系统的阻抗大约是10⁶欧姆。使用该值作为公式中电容的阻抗，忽略公式中的j，f=10Hz：

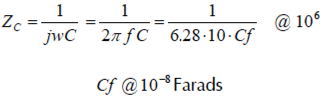
这是第二个初始值。

阻抗谱的中间区域，阻抗曲线趋近于一条水平线处看起来像另一个电阻。这肯定是Rp，我们可以给它赋一个大约为100 kΩ的值。

高频区表现为电容性。10 kHz处的阻抗看似大约为10 kΩ。按照上述的程序走，但是10⁴ Hz处的阻抗设为10⁴欧姆，您就能获得一个大约为10^-9法拉电容值。这是Cc的初始值。

高频数据永远不会变为电阻式，这由阻抗的常数表明。Rμ必须比在高频处使用的阻抗值要小。因此，用1欧姆作为初始值。

现在我们拥有了一组初始值，尝试再来拟合一下。在参数窗口填入初始值。您可以用E的格式输入电容值，例如1E-9表示10^-9。按下Preview按钮。您会看到一个与图4类似的曲线。

需要注意的是种子曲线和实验数据得到的阻抗值和相位角曲线的形状相似。一般而言，每当这些曲线形状相似而且初始值与合适值在100倍的范围内时，模型将能拟合。

当按下Calculate，您可以看到拟合真的非常得好（图5）。表1显示了由拟合器计算所得的参数值，与仿真电解池各元件数值的比较。Levenberg-Marquadt和Simplex算法都给出了相同的结果。

表1 拟合值和元件值

需要注意的是Rμ拟合值存在着很大的不确定性，并且真实Rμ值和拟合值之间符合得比较不好。这很容易解释。我们说过，阻抗曲线永远不会在高频处变成电阻式。事实上，在高频处的轻微幅角变化仅仅表示了Rμ的存在。一条重要的原则是：如果一个元件的阻抗在拟合频率范围内不是电解池阻抗的重要影响因素，该元件的参数值将会不好而且数值的不确定性会比较大。

两种算法都显示了一个“拟合优良度”的值。0.0001（1E-4）这个值表明是非常好的拟合结果，测得阻抗和计算值间仅有大约1%的差异。0.01被视为一个“一般”的拟合结果。差的拟合结果给出的是一个高于或等于0.1的值（30%测试误差）。当不合适的模型被选择时会得到这样的结果，与实验数据符合得不好。您应该另外探索一下其他的假说和模型以解释您的数据。

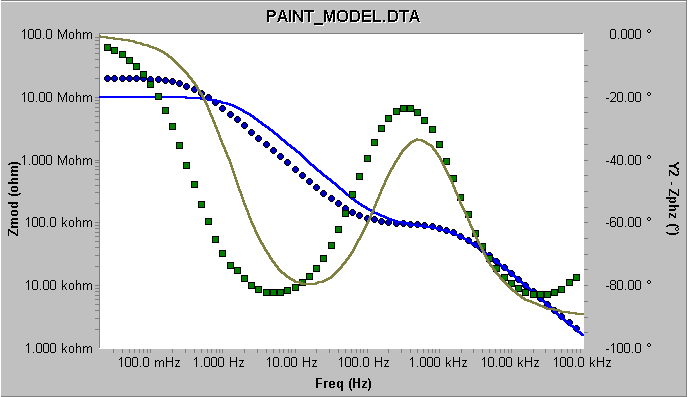
图4 初始值—涂层模型

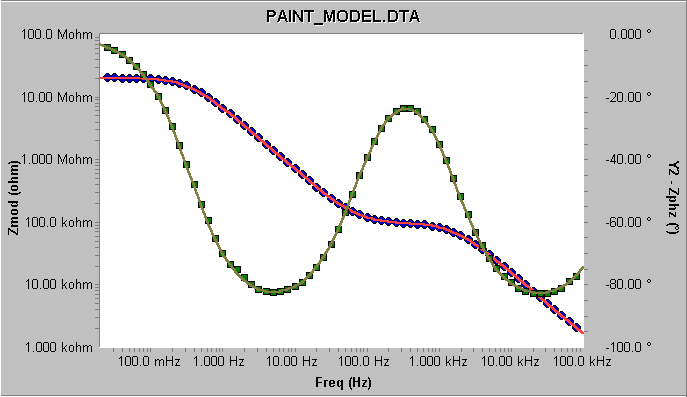
图5 终拟合结果—涂层模型

例2：可再充碱性电池

在这个例子中，开始EIS数据分析前模型还是未知的。样品是一个商业AA可再充碱性电池。在每一个充放电循环后，阻抗谱由Gamry混合EIS模式记录。充电态的EIS阻抗谱比放电态的更加有趣，所以其中一个充电态阻抗谱被选作说明。

第一周充电循环后的阻抗谱如图6（Bode曲线）和图7（Nyquist曲线）所示。Bode曲线展示了与之前例子非常不同的行为，所以它被转换成线性阻抗值以代替更常见的对数值。当频率变化超过3个数量级时，阻抗值的变化小于30%！在对数范围呈现的较小的变化非常令人困惑，所以线性比例被采用。幅角的变化也非常得小—幅角变化小于5º。

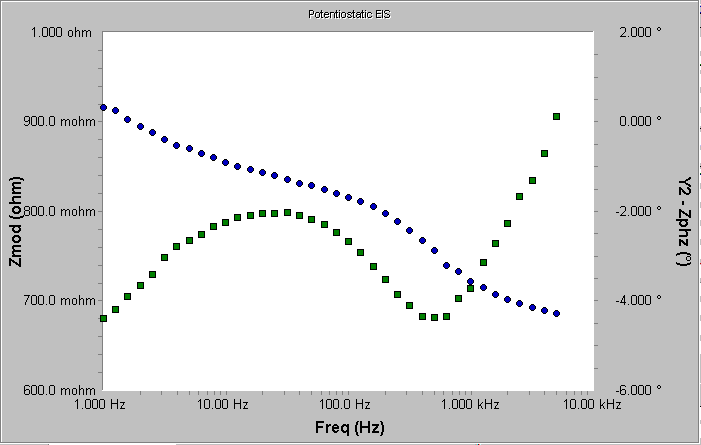
图6 充电态电池的Bode曲线

Nyquist曲线（图7）显示了一个扁半圆，是Randels元件的典型特征。在低频时，曲线显示了一个完整的对角线，与水平线呈45º角，表明是Warburg阻抗。

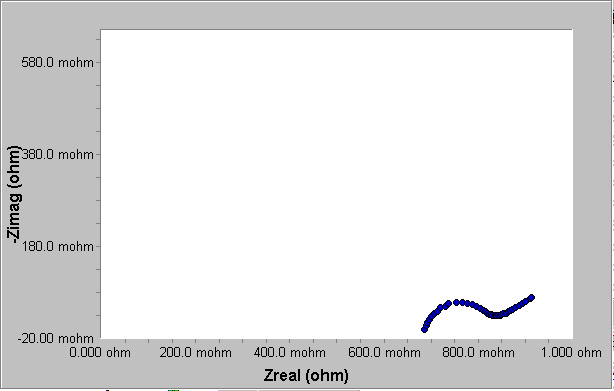
图7 充电电池的Nyquist曲线

什么是该系统模型较好的起始点呢？

我们知道样品是一个用两电极模式测试的电池，所以它拥有两个电极/电解质界面。

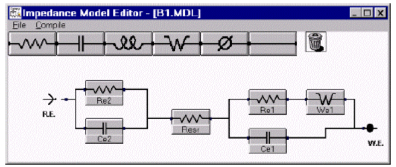
图8 第一个切入模型—电池数据

我们可以假设每一个界面有一个双电层电容和一个电荷转移电阻。让我们将Warburg阻抗给一个界面。

我们也知道电极间的溶液通道也有一个电阻。这是电池的等效串联电阻（esr）。将这些事实和假设代入模型中，我们会得到如图8所示的图解。

再一次，在拟合曲线收敛（一个数学术语表示将得到一个好的拟合结果）前我们需要初始值。看看模型（并暂时忽略Warburg阻抗），高频的极限阻抗是Resr。测试Bode曲线，您会看到在高频处的阻抗大约是0.7 欧姆。使用这个值作为Resr的初始值。

低频阻抗（10 Hz）大约是0.85 Ω。仍旧忽略Warburg阻抗，这个值是R1，R2和Resr的总和。由于我们估算Resr是0.7 Ω，所以R1加R2应为0.15 Ω。我们没有好的方法可以把这两个电阻的贡献分开，因此我们将每一个的初始值设为0.075 Ω。

我们也不能够表面地区分C1和C2的贡献。在6000Hz到100Hz之间，电解池的阻抗变化了0.15Ω，将“中点”1000Hz代入上述电容阻抗方程式中。串联的C1和C2的数值是1mF。串联的电容与并联的电阻相似，所以我们能够給C1和C2分别赋一个初始值为2mF。

当您预览使用这些值并给Warburg系数赋值1.0得到的种子曲线时，您会得到如图9所示的曲线。

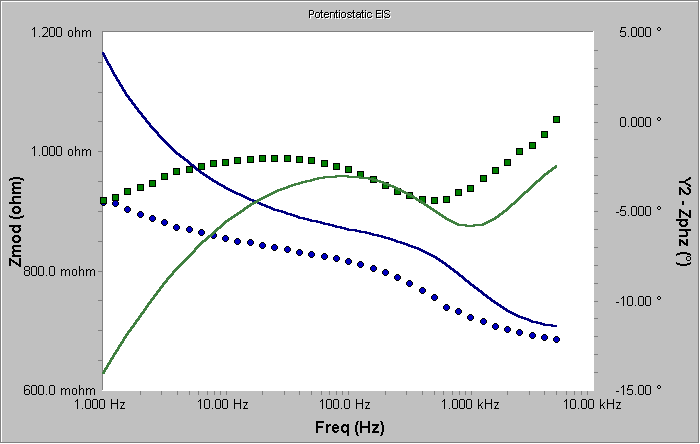
图9 初始曲线的预览—粗略估算

阻抗与相位角曲线都看起来与数据曲线的形状相似，所以如果我们点选了Calculate按钮时，我们就是安全的。

如果我们想要提高初始值，我们应当注意到Warburg元件导致了低频阻抗的增加。降低Warburg系数将会使这个增加在任何给定频率下变小。图10显示了Warburg系数增加到3的初始值曲线。

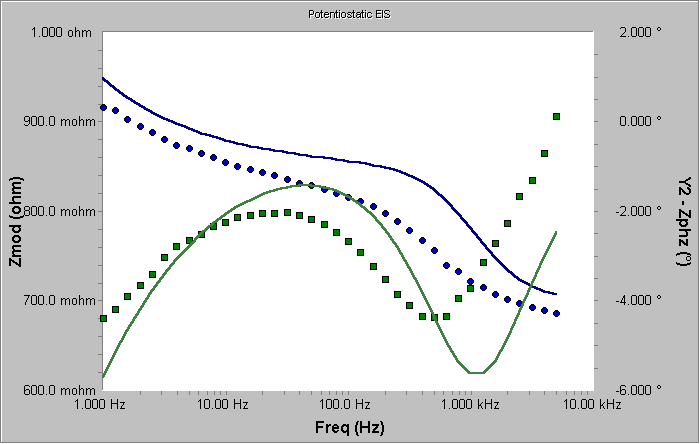
图10 Warburg系数为3的初始曲线

使用任意一组初始值，选择Calculate将得到图11中的曲线

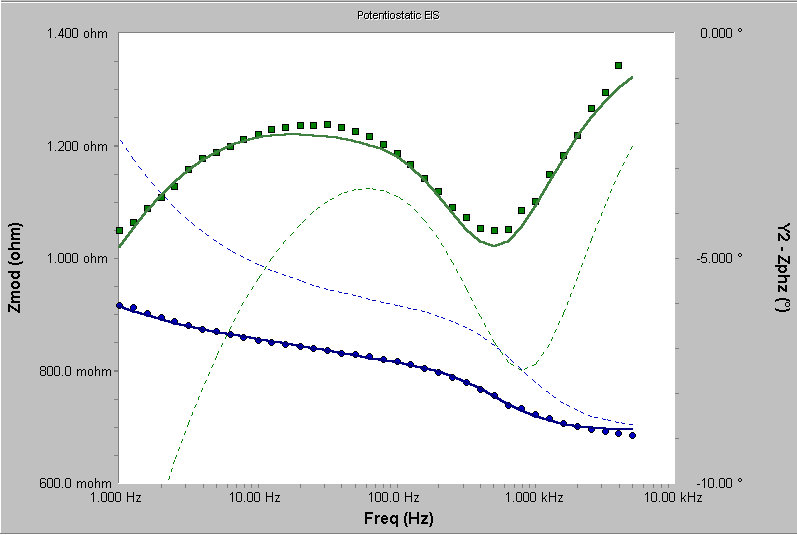
图11 与初始模型进行拟合

拟合结果不太糟，但是有一些明显的误差，尤其是相位角。让我们尝试用恒定相元件（CPE）替代两个电容。新的模型如图12所示。

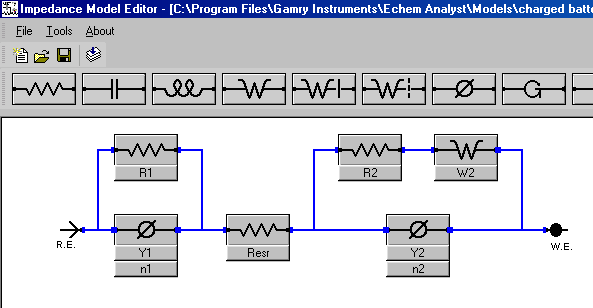
图12 使用CPE的电池模型

我们可以使用前述拟合中寻得的数值来计算新的CPE元件的初始值。前面的拟合数值可以在图11中的表格中查看。请记得第一个CPE参数与电容值相等。因此，Y2的初始值是0.075，Y1的初始值是0.0027。使用1.0作为两个CPE参数α的初始值。

当我们输入这些新的初始值到新的模型中，然后按Calculate按钮，我们可以得到曲线如图13所示。

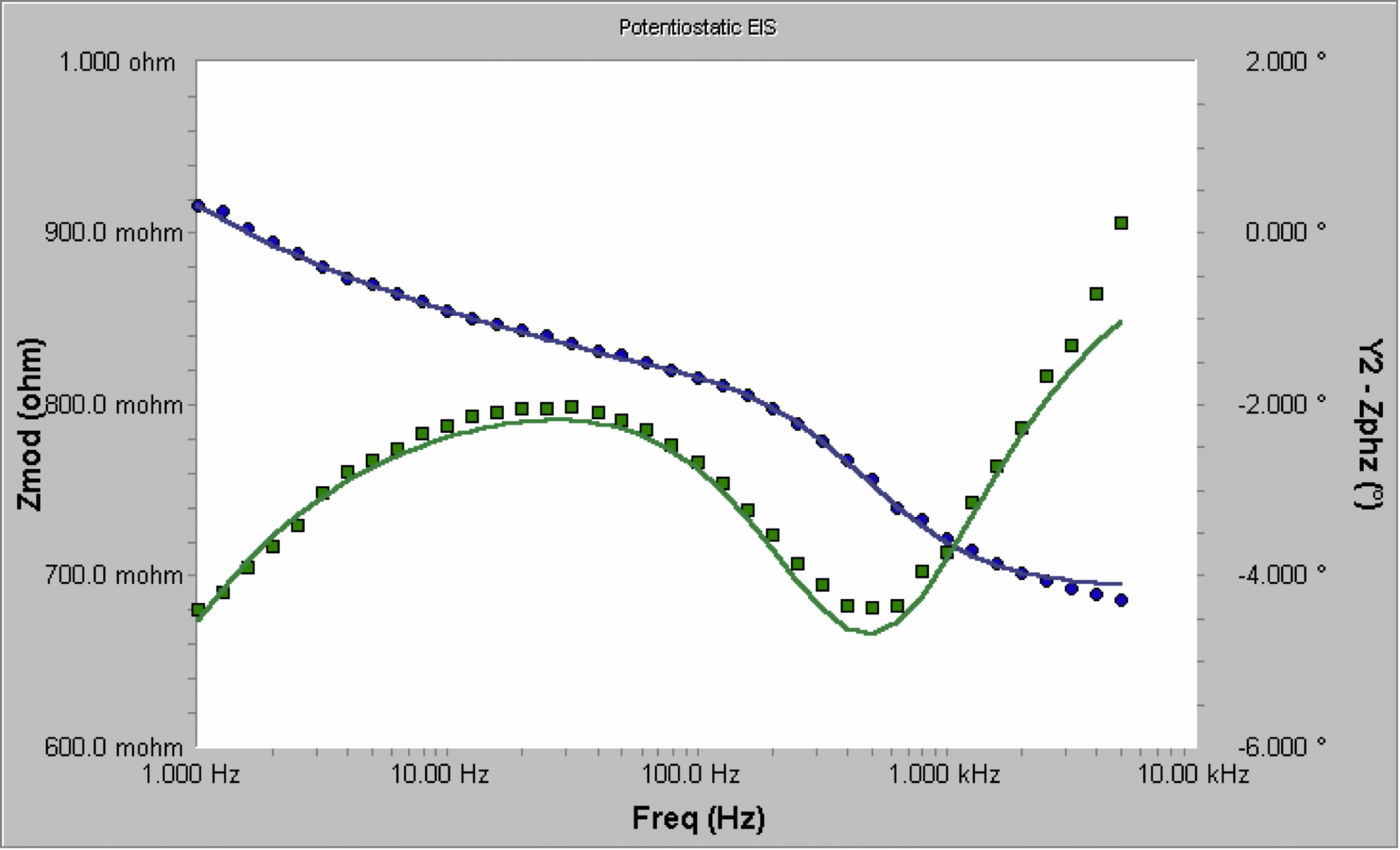
图13 第二切模型拟合

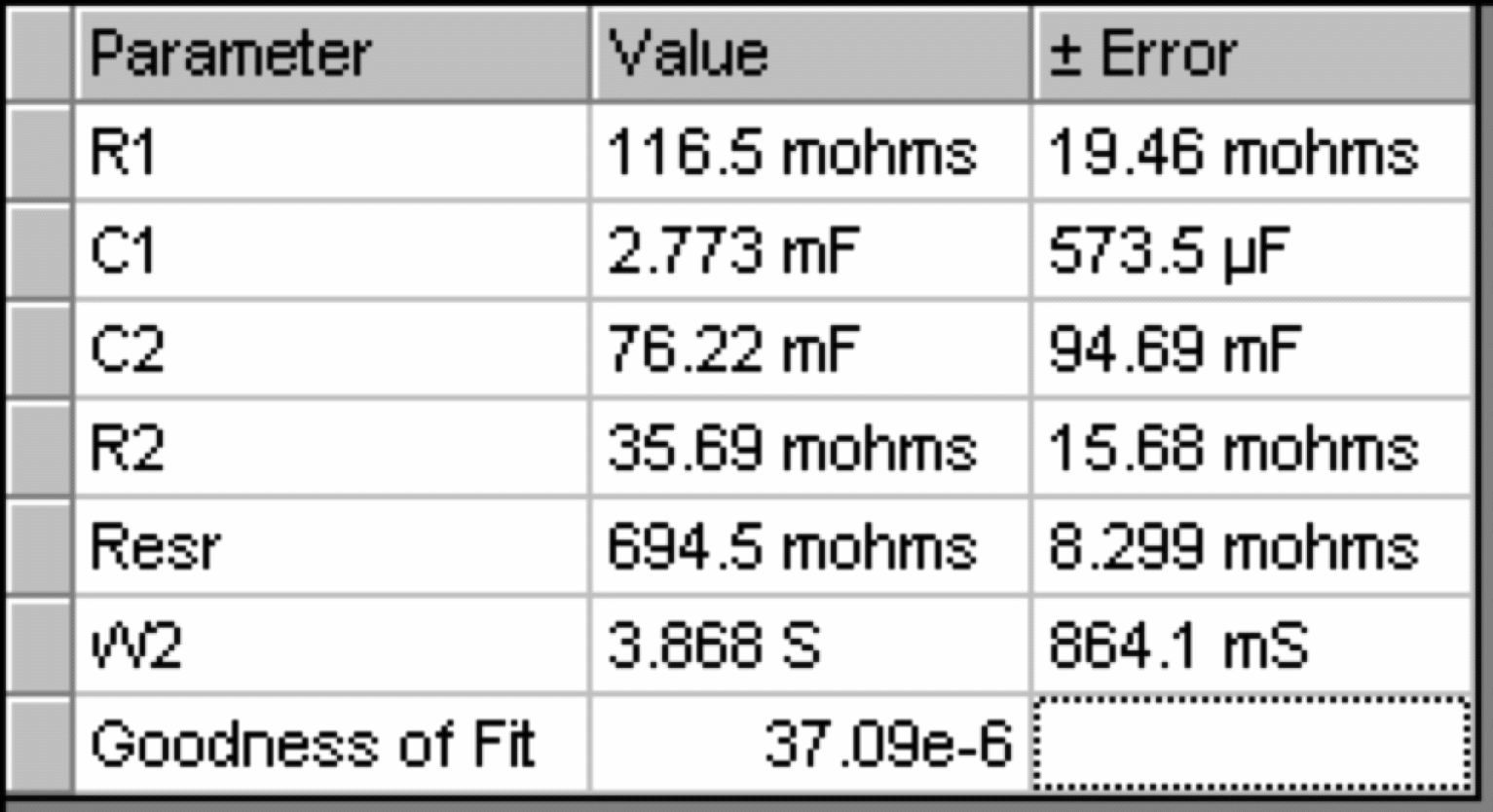
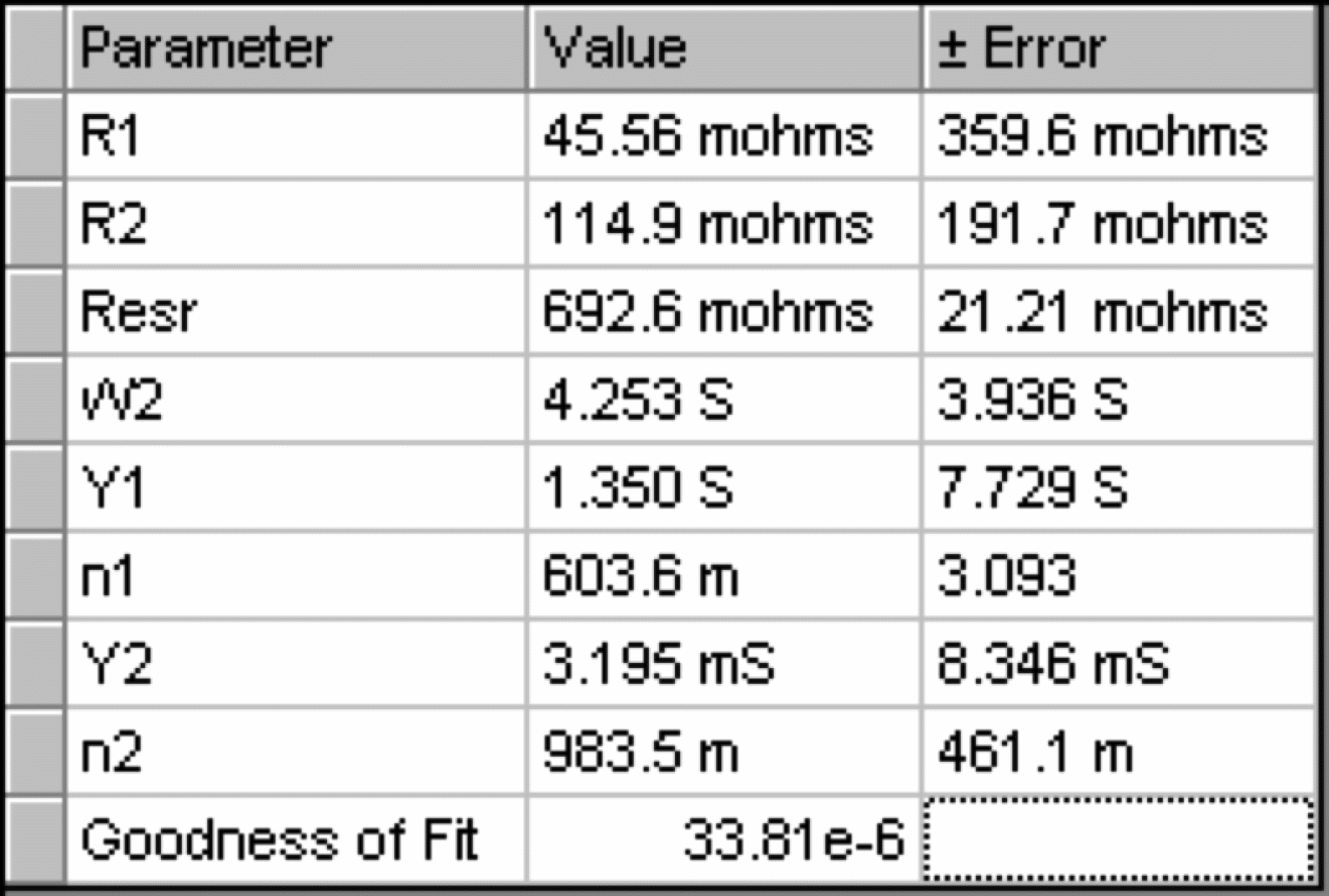
仔细比较图11和图13可以发现，CPE元件略微提高了10Hz到100Hz间的幅角拟合。这个提高可能不够大以证明CPE和它任意参数α的存在。如果我们来看看每一个模型的“拟合优秀”的数值，我们可以把它稍微量化一下。数值都列于下表中拟合结果的后一行。

表2 比较两种电路模型拟合的优良度

两种模型的“拟合优良度”都非常好：两个的值都在1e-4的标准以下，表示拟合良好。不过，两个的数值几乎相等：他们仅相差大约10%。根据经验，如果“拟合优良度”的数值相差少于3个数量级，那两个模型可以被视为“无法区分”。CPE模型应该仅在它的“拟合优良度”数值低于12e-6或（37e-6）/3时才会被考虑。

需要注意的是，当仅有两端EIS测量可用时，我们无法区分电池的负极和正极界面。如果参比电极可以放入电解池，单独界面的阻抗可以被测量。

小结

用EIS模型拟合实验数据是一个非常简单的工作。它仅需要您对您所测电解池及其原理稍微有点儿了解，然后对电解池元件的表现行为有一个基本的认识。

如果您没有一个现成的模型，那就从检测数据开始。寻找相位角中的谷值，它反映的是数据中的拐点。使用您对电解池的了解，参考实验数据提出一个模型。在很多例子中，EIS300提供的标准模型可以提供一个终模型或者一个可以发展您自己的模型的好的起始点。

Gamry不建议您向模型中增加元件直到拟合中所有的可视误差都消除了。模型中如果包含在电解池化学过程中没有任何基础的元件时会得到一个很好的拟合结果，不过这个结果不能够提供关于电解池行为的任何实用信息。

一旦您建立起一个模型，首先估算电阻值。寻找Bode曲线中的水平区域，然后将它们赋成单个的或者串联的电阻。然后按文中的方法估算电容的数值。在您做这些估算时，没必要太精确。任何与真实数值在1个数量级差别以内的数值都是好的起始点。

后，使用预览特征来检查您的估算。此时，您可以微调模型中Warburg阻抗的初始值。一般而言，每当初始曲线与数据曲线的形状相似时，拟合算法将会收敛。如果两者曲线拥有不懂的形状，拟合程序可能失败。

后，执行拟合，检查结果。如果拟合结果看起来不太好，您可能需要调整模型，重复上述过程。

要下载本应用报告的PDF文件吗？

First Name:

Surname:

Email address:

• 电化学交流阻抗谱
• 电池研究
• 腐蚀/涂层
• 能源转化装置
• 研究电化学
• 仪器与硬件
• 石英晶体微天平
•