EIS拟合质量
电化学阻抗谱(EIS)在电化学研究,开发和质量控制领域无处不在。该技术将EIS测试得到的数据与电阻、电容、电感和其他理论元器件组成为的假设电路模型进行比较。如果数据与电路匹配(数据与模型的“拟合”),则这一电路被视为这些数据的有效模型。
有关EIS技术的背景知识,建议您首先阅读我们的应用报告“电化学阻抗谱原理”。有关对EIS数据建立模型的一般讨论,请参考应用报告“使用Gamry EIS软件建立等效电路模型”。
但是,什么构成了用为拟合模型的正确的电子元器件组成的电路?本应用报告讨论了模型中使用过多或不足的组件时的EIS拟合结果。
需要多少参数?
简而言之,答案是足够,但是不要太多。
用足够多的参数可以拟合任意阻抗谱,但是问题就变成了“拟合是否现实?”
除了通过拟合模型得到数据,我们还希望拟合与多孔,绝缘电容层等真实,物理直观的系统相对应。
这些拟合中重要的是能够代表真实的物理系统。其次重要的是模型中每个理想元器件的误差棒小于为该元器件计算出来的值,并且任何剩余误差都不是系统性的,而是随机的。后重要的是拟合度,即χ2值。
基本规则是:使用适合数据的简单模型。不要包含多于的元器件。仅仅是为了提高拟合度而添加电子元器件是不被接受的:这些电子元器件必须在现实世界中具有某种意义。
举例
第一种模型
让我们来看一个例子,一个18650锂离子电池的EIS数据。一下是阻抗数据的Bode图。
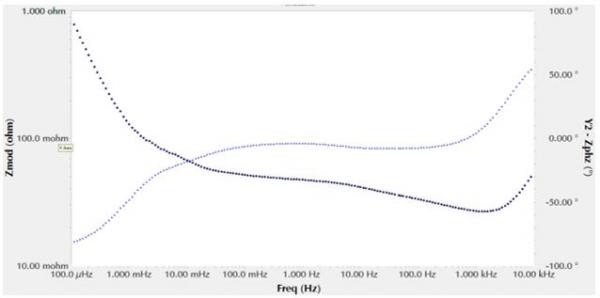
图1 锂离子电池EIS数据的Bode图
我们从某种物理模型开始,如下图所示:
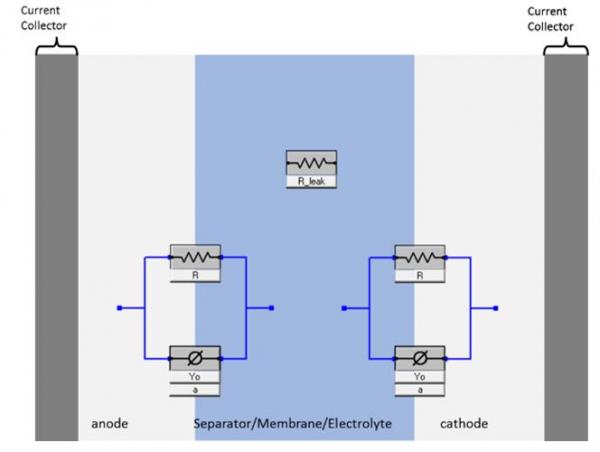 图2 锂离子电池物理模型的原理图,其中电子元器件与电池各个部分相对应
图2 锂离子电池物理模型的原理图,其中电子元器件与电池各个部分相对应
我们添加一个可能与线电容或仪器有关的杂散电容,用Gamry分析软件中阻抗模型编辑创建的由6个电子元器件组成的等效电路图:
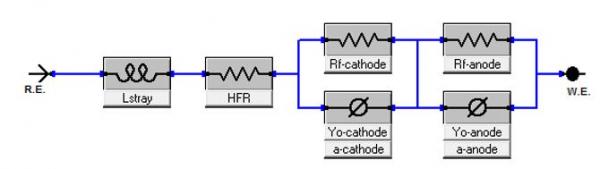
图3 锂离子电池等效电路的第一次迭代
这儿是我们用Gamry Echem Analyst™软件进行拟合:
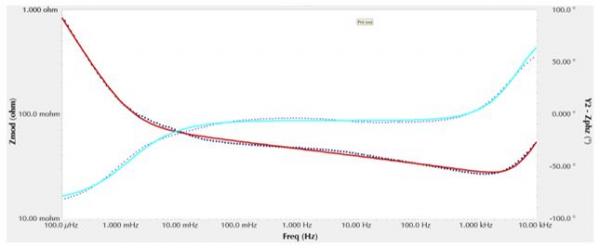
图4 用图3中的等效电路拟合得到的锂离子电池EIS数据
即使一眼就能看出,尽管或多或少再现了数据的形状,但是这一拟合有一些问题。
剩余误差明显不是随机的:
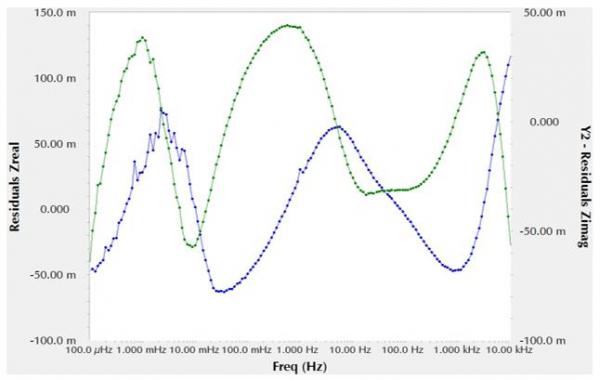
图5 图4中的拟合产生的随机误差
拟合度χ2值为0.00274,令人惊讶的是,这一结果还不错。
总而言之,我们可以看出这一模型是有缺陷的。
第二种模型
现代电池通常设计成较高的表面积与体积之比,即在电解质内具有很多空隙。因此,我们应该在等效电路中包含代表多孔的元器件:
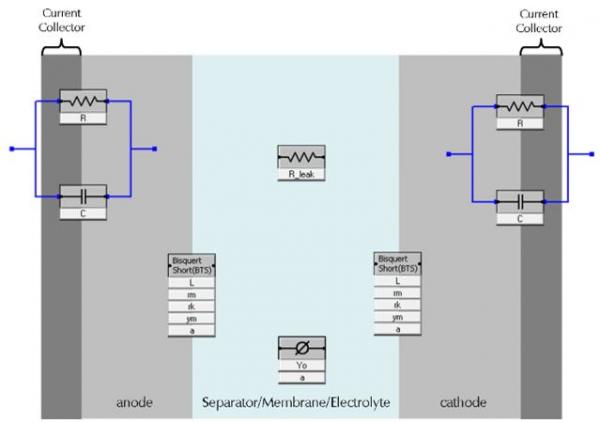
图6 修改后的模型
阳极和电解质之间,以及阴极和电解质之间的界面处的Bisquert元件是无限串联的电阻,与常相位角并联电阻组合在一起。有关Bisquert电子元件的更多信息,请参考我们的应用报告“传输线模型:它们是什么?它们有什么用?”系统总的等效电路为:
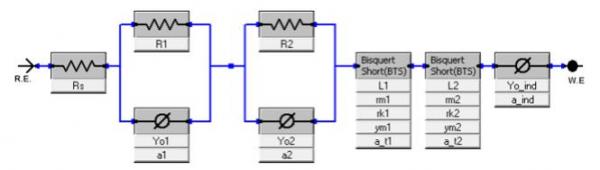
图7 图6中的等效电路图
对于这种看似复杂的系统,只有八个电子元器件。
以下是拟合后的数据。
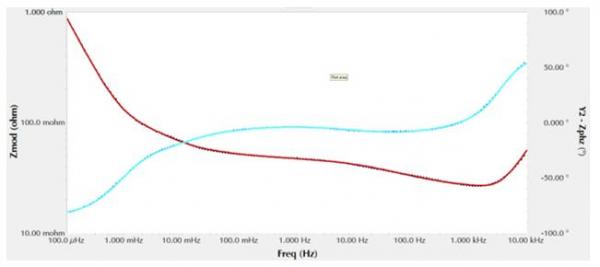
图8 用图7的等效电路拟合出的数据
叠加在数据上的实线(拟合)与原始数据重叠的很好。检查一下剩余误差,看看是否存在系统误差:
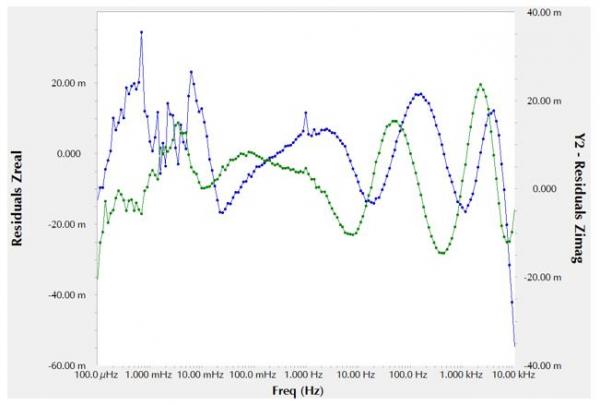
图9 用图7等效电路拟合结果的剩余误差
剩余误差似乎相对随机,以非系统的方式落在零线的上下。不仅如此,它们大约是之前模型的四分之一。拟合度χ2怎么样?
χ2 = 2.253 × 10–4
该值比之前的计算结果小10倍。
因此,我们有理由相信该模型是每个元器件都对应电池一部分,符合物理的模型,具有较好的拟合度和较小的随机剩余误差。
如果在等效电路中添加寄生元器件会如何?
对于第二个模型,让我们串联一个类似杂散电感。拟合看起来大致相同(因此我们不进行复制),但是剩余误差如何?
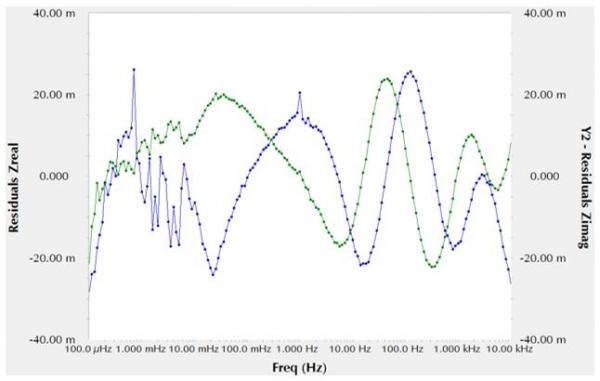
图10 图7中的等效电路添加杂散电感后的剩余误差
仅在高频处有一些轻微的改善。
拟合度χ2为0.00000327,有明显提高。
判断等效电路拟合效果的后一个因素是每个元器件的剩余误差。在这里,我们注意到一些问题。某些元器件的误差明显大于元器件本身的计算值(表1,粗斜体表示)。
表1 图7中等效电路添加杂散电感后的拟合值以及误差值。误差大于计算值的元器件由粗
斜体表示
Component | Value | Error | Unit |
R1 | 0.001266 | 0.1183 | Ω |
R2 | 0.01711 | 0.03101 | Ω |
Yo3 | 1.040 | 1.987 | S×sa |
a4 | 0.7405 | 0.2166 |
|
L5 | 0.9335 | 0.1719 |
|
rm6 | 0.05015 | 0.003484 | Ω |
rk7 | 0.1309 | 0.1115 | Ω |
ym8 | 881.9 | 59.66 | S×sa |
a9 | 0.8004 | 0.001724 |
|
R10 | 23.89 | 28.45 | Ω |
Yo11 | 1532 | 184.2 | S×sa |
a12 | 0.9739 | 0.01860 |
|
L14 | 0.3273 | 0.6177 |
|
rm15 | 0.4677 | 0.3220 | Ω |
rk16 | 0.02744 | 0.1984 | Ω |
ym17 | 0.1676 | 0.2693 | S×sa |
a18 | 0.8714 | 0.7740 |
|
Yo18 | 5718 | 1.961 × 106 | S×sa |
a19 | –0.6792 | 3.478 |
|
L20 | 3.168 × 10–7 | 3.464× 10–6 | H |
因此添加杂散电感元器件可以改善拟合度,但是也可能引起元器件本身值的劣化。在这种情况下我们添加了太多的元器件来拟合数据。
第三种模型
近我们了解到另一种用于锂离子电池阻抗数据拟合的模型:
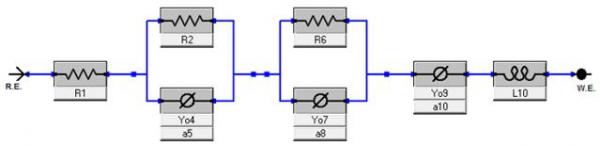
图11 另一种等效电路模型
该模型用简化的电阻和常相位角代替Bisquert,并增加了杂散电感。因此,图6中的界面没有包含在该模型中。
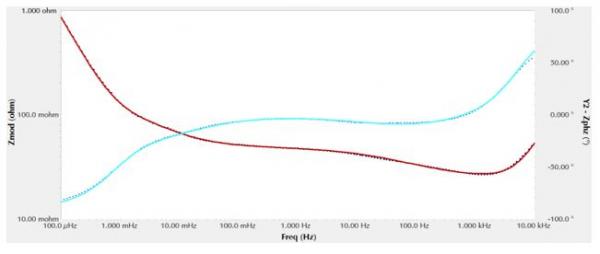
图12 图11等效电路拟合结果
拟合度非常好,为0.0004806。剩余误差相对随机并且很小(虽然不如第二个模型那样小):
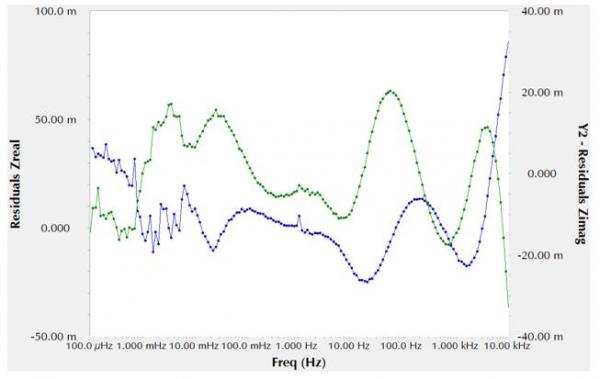 图13 图11等效电路拟合结果的剩余误差
图13 图11等效电路拟合结果的剩余误差
再来看一下元器件的误差(表2):
表2 等效电路拟合值及其误差
Component | Value | Error | Unit |
R1 | 0.02488 | 4.444 × 10–4 | Ω |
R2 | 0.02375 | 1.106 × 10–3 | Ω |
Yo4 | 1.813 | 0.3058 | S×sa |
a5 | 0.5733 | 0.03191 |
|
R6 | 0.04811 | 6.692 × 10–3 | Ω |
Yo7 | 246.8 | 38.65 | S×sa |
a8 | 0.6856 | 0.04822 |
|
Yo9 | 1856 | 154.1 | S×sa |
a10 | 1.000 | 0.01178 |
|
L10 | 7.574 × 10–7 | 1.287 × 10–8 | H |
*值比计算值大,这是我们对模型有信心。
但我们考虑包含12个自由参数的第三种模型,以及包含20个自由参数的第二种模型,两种模型都给出了类似的结果,我们倾向于接受第三种模型。这并不意味着第三种模型是锂离子电池可接受的模型。根据电池的化学成分和内部组件,可能有不同模型。
结论
创建等效电路拟合阻抗数据时,注意以下几个因素:
- 每个理想元器件的物理性质:是否有存在的原因?
- 每个元器件的误差。是否误差小于元器件本身的值?
- 拟合度:是否相对较小?
Application Note Rev. 1.0 1/8/2020 ©Copyright 2018 Gamry Instruments, Inc. Echem Analyst is a trademark of Gamry Instruments, Inc.
这儿是我们用Gamry Echem Analyst™软件进行拟合:




